Cómo realizar un estudio completo de una función paso a paso
Realizar un estudio completo de una función es un proceso fundamental en matemáticas, especialmente en segundo de bachillerato. Este estudio nos permite comprender en profundidad el comportamiento de una función, sus características y cómo se relaciona con diferentes variables. En este artículo, detallaremos cada paso necesario para llevar a cabo un estudio exhaustivo de una función, desde la determinación del dominio hasta el análisis de las asíntotas, puntos críticos y la curvatura.
Determinación del dominio de la función
El dominio de una función es el conjunto de todos los valores posibles de la variable independiente (normalmente denotada por x para los cuales la función está bien definida. Para determinar el dominio de una función, la forma de resolución depende el tipo de función que estemos tratando; no se resuelve igual para un polinomio, que para un logaritmo o la mezcla de varios tipos. En este video os dejo la resolución del dominio de una función radical.
Cálculo de la imagen o recorrido de la función
La imagen de una función es el conjunto de todos los valores que la función puede tomar al variar su variable independiente.
Cálculo de puntos de corte y signo de una función.
Cortes en el eje X: Son los puntos de la forma (x,0), se obtienen resolviendo la ecuación f(x) = 0.
Cortes en el eje Y: Son los puntos de la forma (0,y), se obtienen ejecutando f(0), es decir, sustituimos la x de la función por cero, y el resultado es el valor de y.
En cuanto al signo de una función nos referimos a donde se encuentra en cada intervalo, es decir, si en un intervalo se encuentra encima del eje x o debajo.
El signo de una función es positivo si f(x) > 0, y es negativo si f(x) < 0.
Cálculo de las simetrías y periodicidad.
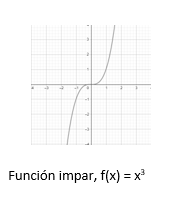
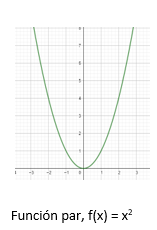
Algunas funciones tienen simetrías, hay de dos tipos, pares e impares.
Ramas infinitas y asíntotas.
En este punto se calculas las asíntotas verticales, horizontales y oblicuas si las hubiera. Para ello echamos mano de los límites de la función y para las ramas parabólicas comprobamos como se comporta la función en los extremos positivos y negativos.
Monotonía de una función.
En cuanto a la monotonía de una función, no es más que simplemente los intervalos de crecimiento y decrecimiento de dicha función, es decir, vamos a comprobar ayudándonos de la primera derivada de la función como se comporta en los intervalos que nos aparezcan después de realizar la derivada e igualarla a cero. Algunos de estos puntos pueden ser extremos relativos de la función. Estos extremos, pueden ser máximos y mínimos relativos.
Curvatura de una función.
En esta parte analizamos los intervalos de concavidad y convexidad de la función. Para ello usamos la segunda derivada donde, al igualarla a cero, sacamos unos puntos, llamados candidatos a ser puntos de inflexión de la función.
representamos la función
Por último hacemos el dibujo aproximado de la función. Para ello, usamos la información de todos los pasos anteriores y la dibujamos a mano alzada. Para una representación más exacta podemos ayudarnos de programas donde se realiza el dibujo más óptimo. https://www.geogebra.org/classic?lang=es
En nuestra web, podrás encontrar una explicación más detallada y con muchos ejemplos de cada uno de los pasos aquí descritos, con el objetivo de sacar tu mejor versión para que rindas en tu próximo examen de bachillerato o ebau.

